Glossary
Browse the IADC Lexicon alphabetically or by category. Get comprehensive definitions of drilling industry terms.
Detection Method
Definition(s)
Detection Method
method or activity by which a failure is discovered Note 1 to entry: A categorization of detection methods (e.g. periodic testing or continuous condition monitoring) is shown in ISO 14224:2006[15], Table B.4. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMaintenance Concept
Definition(s)
Maintenance Concept
definition of the maintenance echelons, indenture levels, maintenance levels, maintenance support, and their interrelationships Note 1 to entry: The maintenance concept provides the basis for maintenance planning, determining supportability requirements and developing logistic support. Note 2 to entry: A maintenance echelon is a position in an organization where specified levels of maintenance are to be carried out (e.g. field, repair shop, manufacturer facility). [SOURCE: IEC 60050‑191] Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMultiple Safety Systems
Definition(s)
Multiple Safety Systems
safety system comprising several sub safety systems operating one after the other when the prior ones have failed Note 1 to entry: Industrial processes often implement multiple safety systems (safety layers). In this case the failure of an intermediate safety layer provokes a demand on the proximate succeeding safety layer and so on. The accident occurs only if the demand is transmitted until the ultimate safety layer and it fails to operate. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsContinuous Mode of Operation Safety System
Definition(s)
Continuous Mode of Operation Safety System
safety system designed to achieve its safety action permanently Note 1 to entry: With a continuous mode safety system the hazardous event occurs as soon as the safety system fails. This is illustrated in Figure B.1 where the systems states “KO” and “hazardous event” are gathered into a single state. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsDemand Mode of Operation Safety Systems
Definition(s)
Demand Mode of Operation Safety Systems
safety system designed to achieve its safety action only when receiving a specific request from its surrounding environment Note 1 to entry: Such systems spend most of their time in stand-by position but need nevertheless to be ready to work as soon as a demand occurs. Note 2 to entry: Such systems are subject to hidden failures. Diagnostic and periodic tests are generally implemented in order to reveal the corresponding latent faults. Note 3 to entry: When the demand frequency increases, an on-demand mode safety system may be assimilated to a continuous mode of operation systems. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsRandom Failure
Definition(s)
Random Failure
failure, occurring in a random way Note 1 to entry: A random failure may be time or demand dependent. Whether it occurs or not is not predictable with certainty but the corresponding failure rate (see 3.1.18) or probability of a failure due to demand (see 3.2.13) may be predictable and this allows probabilistic calculations. EXAMPLE Examples of failure mechanisms leading to unpredictable failure occurrence are: hardware random failures resulting from degradation mechanisms; human random failure resulting from error in routine operation, lack of attention, stress, tiredness, etc Note 2 to entry: From the probabilistic point of view, the random failures are the contrary of systematic failures (see 3.2.17) which occur in a deterministic way (i.e. with a probability equal to 1) when some conditions are met. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsCommon Mode Failures
Definition(s)
Common Mode Failures
failures of different items, occurring in the same way Note 1 to entry: Common mode failures may have different causes. Note 2 to entry: Common mode failures can be due to common cause failures Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsFailure Due to Demand
Definition(s)
Failure Due to Demand
failure occurring on demand γ, ψ failure of one item due to a change of its state triggered by an external event (the so-called “demand”) EXAMPLE 1 Obtaining 2 when launching a dice is an event occurring on demand. The probability of this event is 1/6. It does not depend on the elapsing time but only of the demand itself (i.e. the fact that the dice is launched). EXAMPLE 2 The failure of an electromechanical relay (e.g. rupture of the spring) when it changes state depends on the number of operations (cycles) rather on the operating time (see IEC 61810–2[49]) and this is the same for the failure of an electronic device due to over voltage when it is switched or the blocking of a diesel engine when it is started, etc.: these are typical examples of failures due to demands (or cycles). Note 1 to entry: In this Technical Report two kinds of demand are considered: the periodic tests and the demand for an actual safety action. The probability of a failure due to periodic test is a constant number noted γ and the probability of a failure due to one actual demand of the safety action is a constant number noted ψ. Over a given time interval, those probabilities of failure do not depend on the duration but on the number of demands or tests occurring within this interval. The use of γ and ψ is explained in 7.3. Note 2 to entry: This should not be confused with the “failure on demand” appearing in the term “probability of failure on demand” (see 3.1.14, Note 2 to entry) used in functional safety standards[2] for low demand mode safety systems. In those standards this means “failures likely to be observed when a demand occurs”. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsTime-dependent Failure
Definition(s)
Time-dependent Failure
failure occurring with a probability depending of the time Note 1 to entry: The unreliability F(t) is a typical probability function describing time-dependent failures Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsImmediately Revealed Failure
Definition(s)
Immediately Revealed Failure
overt failure detected failure evident failure failure which is immediately evident to operations and maintenance personnel as soon as it occurs Note 1 to entry: The immediately revealed failures show themselves immediately, but the hidden failures which are quickly detected by specific diagnostic tests are generally considered as immediately revealed failures. Note 2 to entry: The repair of immediately revealed failures may begin immediately after they have occurred. Note 3 to entry: The failures which are detected by periodic tests are not considered as immediately revealed failures. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsCatalectic Failure
Definition(s)
Catalectic Failure
sudden and complete failure Note 1 to entry: This term has been introduced by analogy with the catalectic verses (i.e. a verse with seven foots instead of eight) which stop abruptly. Then, a catalectic failure occurs without warning and is more or less impossible to forecast by examining the item. It is the contrary of failures occurring progressively and incompletely. Note 2 to entry: Catalectic failures characterize simple components with constant failure rates (exponential law): they remain permanently “as good as new” until they fail suddenly, completely and without warning. Most of the probabilistic models used in reliability engineering are based on catalectic failures of the individual component of the system under study (e.g. Markovian approach). Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsSystemic Failure
Definition(s)
Systemic Failure
holistic failure failure at system level which cannot be simply described from the individual component failures of the system Note 1 to entry: Systemic/holistic principles have been concisely summarized by Aristotle by “The whole is more than the sum of its parts”. Note 2 to entry: Components have only failure modes. Those failure modes become dangerous, safe or spurious only when the components are implemented into a safety “system”. This is why dangerous, safe or spurious failures are typical systemic failures. For example the failure “fail to close” of a valve is dangerous only if it belongs to a safety system closing this valve on demand. Otherwise this failure mode does not matter. Note 3 to entry: “Systematic” failures (i.e. occurring in a deterministic way when given conditions are encountered, see 3.2.17) and “systemic” failures should not be confused. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsSystemic Failure
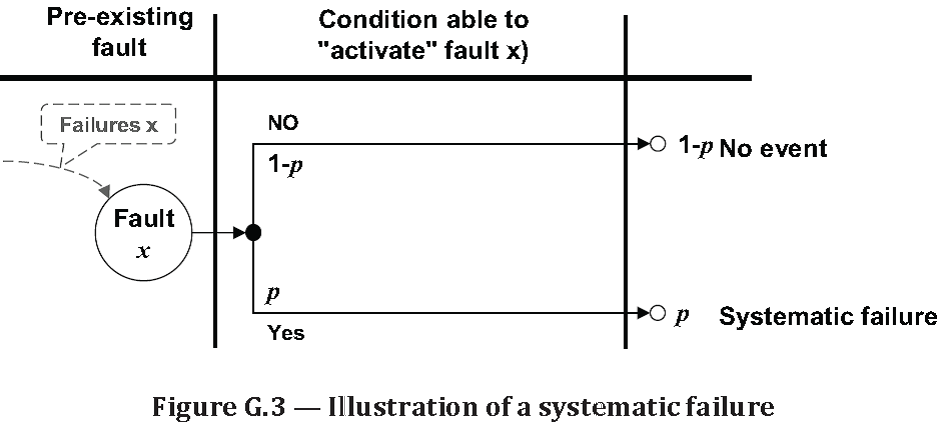
failure that consistently occurs under particular conditions of handling, storage or use Note 1 to entry: The cause of a systematic failure originates in the specification, design, manufacture, installation, operation or maintenance. Its occurrence is precipitated by particular conditions of handling, storage, use or maintenance (see Figure G.3) Note 2 to entry: Corrective maintenance without modification will usually not eliminate the failure cause. Note 3 to entry: A systematic failure can be reproduced by deliberately applying the same conditions, e.g. in verifying the failure cause (from IEC 60050–191 ed3[14]). Systematic failures are non-random failures (see 3.2.16). Note 4 to entry: In operation, a systematic failure is a manifestation of a systematic fault (i.e. a pre-existing state of the system). Note 5 to entry: The software systematic failures, called “bugs”, are example of systematic failures: they are due to pre-existing bugs (i.e. faults) and they occur when the input data activate them. Note 6 to entry: Systematic and systemic (which means “at system level”) failures (see 3.2.8) should not be confused. [SOURCE: IEC 60050‑191]
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsCritical Safe Failure
Definition(s)
Critical Safe Failure
spurious failure of a safety system, due to safe failure(s) of its component(s), triggering the safety action and leading to a spurious safety action Note 1 to entry: The concept of critical safe failure is illustrated in Figure B.1. Note 2 to entry: This is a systemic failure in relationship with a given safety action performed by the safety system. This concept is irrelevant for an individual item on the shelves. Note 3 to entry: The same failure of a component belonging to a safety system may be safe or spurious (critical safe) depending of the system state from which it occurs (e.g. the safe failure of a sensor belonging to 2oo3 is only safe when it occurs in 1st position. It is critical when it occurs in 2nd position).
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsSpurious Failure
Definition(s)
Spurious Failure
failure triggering an action in an untimely manner Note 1 to entry: Critical safe failures (see Figure B.1) are the typical spurious failures related to safety systems. Note 2 to entry: A spurious failure does not necessarily imply a spurious trip (3.4.14) but a spurious trip is always the result of a spurious failure.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsSafe Failure
Definition(s)
Safe Failure
failure of a safety system which tends to favour a given safety action Note 1 to entry: The concept of safe failure is illustrated in Figure B.1. Note 2 to entry: A failure is safe only with regard to a given safety function. This is a systemic failure in relationship with a given safety action performed by the safety system. This concept is irrelevant for an individual item on the shelves. Note 3 to entry: The non-critical safe failures basically increase the probability of success of the safety function. The critical safe failures initiate the related safety actions when this is not needed (see spurious failures).
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsCritical Dangerous Failure
Definition(s)
Critical Dangerous Failure
dangerous failure leading to the complete inhibition of the safety action (i.e. leading to a dangerous situation for the protected system) Note 1 to entry: This is a systemic failure in relationship with a given safety action performed by the safety system. Therefore this concept is irrelevant for an individual item on the shelves. Note 2 to entry: The same failure of a component belonging to a safety system with internal redundancy may be dangerous or critical dangerous depending on the system state from which it occurs. Note 3 to entry: The critical dangerous failures that are undetected (e.g. those revealed by periodic tests) are sometimes called safety critical failures (cf. ISO 14224[15]). The equipment subject to such potential failures can be identified within a plant and monitored, and the ratio between the number of safety critical failures detected by periodic tests and the corresponding number of tests performed (commonly called “ failure fraction”) is being used for that purpose. This indicator of the average unavailability (PFDavg) due to dangerous undetected failures is established by using test reports. It is important not to mix such failure fraction with other reliability terms. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsDangerous Failure
Definition(s)
Dangerous Failure
unsafe failure failure of a safety system which tends to impede a given safety action Note 1 to entry: This is a systemic failure in relationship with a given safety action performed by the safety system. Therefore this concept is irrelevant for an individual item on the shelves. Note 2 to entry: See Figure B.1.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsFailure Classification
Definition(s)
Failure Classification
Explanations about the various states and the various failures of a safety system are developed in Annex B. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsRestoration Rate
Definition(s)
Restoration Rate
μc onditional probability per unit of time that the restoration of a failed item ends between t and t+dt, provided that it was not finished over [0, t] Note 1 to entry: The following relationship holds when the restoration rate is constant: MTTRes = 1/μ. Note 2 to entry: The “restoration” rate is in relationship with the restoration time. Similarly the “repairing” rate can be defined in relationship with the “overall repairing” time and the “active repair” rate in relationship with the “active repair” time. Note 3 to entry: The restoration rate has the same mathematical properties for the restoration as the failure rate for the failures. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Time to Demand
Definition(s)
Mean Time to Demand
expected time before the demand on the safety system occurs. Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMaximum Permitted Repair Time
Definition(s)
Maximum Permitted Repair Time
MPRT maximum time allowed to repair a fault before undertaking an action to make the risk disappearing EXAMPLE When a dangerous fault is revealed for a safety system operating in demand mode, it may be decided to reach a safe state when a maximum duration has elapsed: a MPRT of 8 h means, for example, that if the repair is not completed after 8 h, the process is shut down. Then a safe state is reached, the fault is no longer dangerous, and it is not necessary to take into account the remaining time spent to complete the repair. This is illustrated in Figure 6, Figure 7 and Figure B.1. When the fault may result of several failure modes, the MPRT allows to repair those within short MRT without shutdown of the process. Note 1 to entry: When a MPRT is defined as a maintenance procedure it is necessary to take it into consideration for the probabilistic calculations of hazardous events. Reciprocally it is necessary that this MPRT be respected during the actual repair actions in order to keep the probabilistic calculations valid. Note 2 to entry: The role of the MPRT is close to the role of the MTTS (see 0). The difference is that the MPRT is a maximum duration allowed to reach a safe state and the MTTS is the average duration needed to reach the safe state when a dangerous fault is revealed (see Figure 6 and Figure 7). The methods developed in this Technical Report have been focused on random repair values (MTTRes, MRT, MTTS) rather than on deterministic values (MPRT), but the MPRT can be easily handled by using Petri nets and Monte Carlo simulations.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Time to Safe State
Definition(s)
Mean Time to Safe State
MTTS expected time needed for the protected installation to reach a safe state after a dangerous failure of a safety system has been detected EXAMPLE When a dangerous fault is revealed for a safety system operating in demand mode, it may be decided to reach a safe state rather to undertake the repair of the fault and this may take some time: a MTTS of 8 h means, for example, that, on average, 8 h are needed to shut down the process. After the shut down, a safe state is reached, the fault is no longer dangerous and it is not necessary to take into account the remaining time spent to complete the repair. This is illustrated in Figure 6, Figure 7 and Figure B.1. Note 1 to entry: When the MTTS is defined as a maintenance procedure it is necessary to take it into consideration for the probabilistic calculations of hazardous events. In this case the MTTS replaces the MRT (see 3.1.33) with regard to the probabilistic calculations. Reciprocally it is necessary to verify that this MTTS is respected during the actual repair actions in order to keep the probabilistic calculations valid. Note 2 to entry: The role of the MTTS is close to the role of the MPRT. The difference is that the MPRT is a maximum duration allowed to reach a safe state when the MTTS is the average of the random duration of the TTS needed to reach the safe state when a dangerous fault is revealed (see Figure 6 and Figure 7). The methods developed in this Technical Report have been focused on average random values (MTTRes, MRT, MTTS) rather than on deterministic values (MPRT), but the MPRT can be easily handled by using Petri nets and Monte Carlo simulations.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Fault Detection Time
Definition(s)
Mean Fault Detection Time
MFDT expected time needed to detect a fault Note 1 to entry: The MFDT is the time a) in Figure 5, Figure 6 and Figure 7. Note 2 to entry: The MFDT is equal to zero for immediately revealed failure; (see Figure 6) generally negligible for quickly detected failures; (see Figure 6) depending of the test policy for the hidden failures. In this case it may be the main part of the item down time (see Figure 7). Note 3 to entry: The MFDT used in this Technical Report should not be mixed-up with the mean fractional dead time which has the same acronym.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Active Repair Time
Definition(s)
Mean Active Repair Time
expected active repair time Note 1 to entry: The MART is the expected effective time to repair c, (see Figure 5, Figure 6 and Figure 7).
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Overall Repairing Time
Definition(s)
Mean Overall Repairing Time
MRT expected time to achieve the following actions: • the time spent before starting the repair b; and, • the effective time to repair c; and, • the time before the component is made available to be is put back into operation d Note 1 to entry: See Figure 5, Figure 6 and Figure 7. Note 2 to entry: The terms “repair”, “repairable”, “repaired” used in this Technical Report, unless otherwise specified, are related to the overall repairing time (see Figure 5). Note 3 to entry: When a safety system operating in demand mode is faulty, the risk disappears as soon as the protected installation is placed in a safe state (e.g. stopped). In this case (see Figure 6 and Figure 7) the MTTS replaces the MRT (see 3.1.36) with regard to the probabilistic calculations. Note 4 to entry: This definition is in line with IEC 61508[2] but not with IEC 60050–191.[14].
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global StandardsMean Time to Restoration
Definition(s)
Mean Time to Restoration
MTTRes expected time to achieve the following actions: (see Figure 5, Figure 6 and Figure 7): • the time to detect the failure a; and, • the time spent before starting the repair b; and, • the effective time to repair c; and, • the time before the component is made available to be put back into operation d Note 1 to entry: Figure 5 illustrates how the times a, b, c and d defined in the IEC 61508[2] standard are linked to the delays defined in the IEC 60050–191[14] standard. Time b starts at the end of a; time c starts at the end of b; time d starts at the end of c. Note 2 to entry: Figure 5, Figure 6 and Figure 7 can be used to understand the differences between the definitions of MTTRes, MRT and MART used in this Technical Report. Note 3 to entry: The MTTRes is linked to the MRT and the MFDT by the following formula: MTTRes = MFDT + MRT.
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global Standards
Mean Down Time
Definition(s)
Mean Down Time
expectation of the down time Note 1 to entry: See Figure 3 and also ISO 14224[15] or IEC 60050–191[14] for definitions of up time and down time. [SOURCE: IEC 60050 −191]
Source: ISO/TR 12489:2013(E) Reliability modelling and calculation of safety systems. Global Standards